Water Distribution
System Toolkit
Software: Graphical Representation and Analysis
It has become possible for many small utilities to develop or utilize hydraulic network models in their day-to-day planning and operational activities. In addition to determining pressures and flows within a particular system, such models can be used to address the issues of fire-flow capacity, system reliability, rehabilitation scheduling, emergency response, and energy management. In most cases, the costs associated with network modeling will be more than offset by better operation and management decisions that will result from a more comprehensive understanding of the network system.
Despite such advantages, many utilities do not feel like they have the technical background, staff or budget to develop and use a water distribution system computer model on a regular basis. As a result, an intermediate tool, called the Graphical Flow Model has been developed for use by such utilities to help them get started up this ladder of improved operational control.
Graphical Flow Model
The Graphical Flow Model (GFM) has been developed for water utility managers as a first step toward utilizing a computer model of their distribution system. The GFM is not a comprehensive water system model, modeling all possible aspects of operations; however, for systems that have little to no computer based representations of their system, the GFM is a great asset. First, it provides a graphical representation of a system within an interactive interface, capable of storing and manipulating data pertaining to many components of the system. Secondly, given certain hydraulic operational control inputs, the GFM is capable of returning output for many important system questions such as flow directions and magnitudes, pressures, hydraulic grade line contours, and more.
The GFM has been designed to allow the use of pre-developed GIS datasets in constructing graphical representations of water distribution systems. In particular, the model has been developed to allow use of the Kentucky Infrastructure Authority (KIA) water distribution system database. Finally, the GFM has an option that will allow the user to export any model developed within the GFM graphical user interface (GUI) for possible subsequent use with comprehensively functional water distribution network analysis software (i.e. KYPIPE).
Data Sources
One of the unique challenges of developing computer models for small utilities is the ability to generate and assemble the required basic network data. The Kentucky Infrastructure Authority (kia.ky.gov) has assembled extensive GIS data sets for all of the water distribution systems within the state (http://kia.ky.gov/wris/data.htm). This information includes data on pipelines, water tanks, water treatment plants, water meters, and pump stations. The GFM model includes functionality to upload such data via a graphical user interface to permit the creation of a schematic of the water distribution system.
The existing infrastructure can be displayed in graphical form superimposed on a topographic map. The topographic map can display the physical relationships that the existing system infrastructure has with its surroundings in terms of elevations and natural and urban geographical features. The GFM has been designed with the capability to upload a background map that would contain such information.
Downloading and installing the Graphical Flow Model
The Graphical Flow Model and associated users manual can be accessed below. The user should first download the user's manual and read the appendix that describes how to download the computer program to the user's computer.
Downloading and installing the Network Decontamination Model
In addition to the Graphical Flow Model, a Network Decontamination Model has also been developed for use by water utilities. This model can be used to help determine which valves should be shut to isolate part of the water distribution system in response to a pipe break or a contamination event. The program has been developed to use the same data files generated using the Graphical Flow Model. The user should first download the user's manual and read the appendix that describes how to download the computer program to the user's computer.
Network Analysis Software
Computer models for use in the analysis and design of water distribution systems have been available since the mid 1960's. Such models are typically composed of three parts: a database (composed of both graphical and physical data), a computer program (which solves both hydraulic and water quality equations), and a graphical user interface (see Figure 1).

Figure 1 Network Computer Model
The physical database will contain information that describes the physical infrastructure of the network, system demands, and the operational characteristics of the system. The actual physical characteristics of the network are typically represented in the computer using a node-link representation, where each pipe segment is represented by a line that is joined at both ends by a node (Figure 2). Observed or assumed water demands along the pipe line are normally averaged and then assigned to the nodes (see Figure 3). Additional components, such as tanks, valves and pumps are then represented in the model by treating them either as a special node or pipe element. The graphical database will contain information on the spatial location of the physical components of the system (see Figure 4). The Graphical Flow Model has been especially designed to take advantage of the Kentucky Infrastructure Authority graphical and physical databases for use in building a water distribution system model.
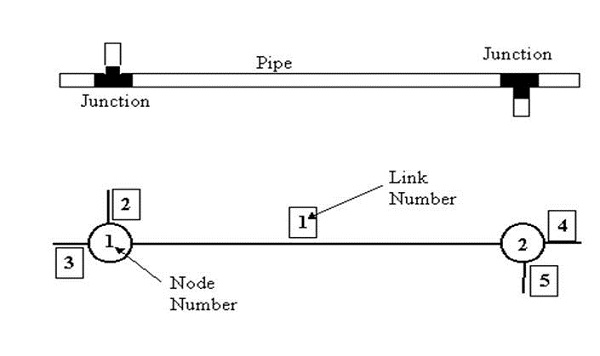
Figure 2 Pipe (link), Junction (node) Conceptualization
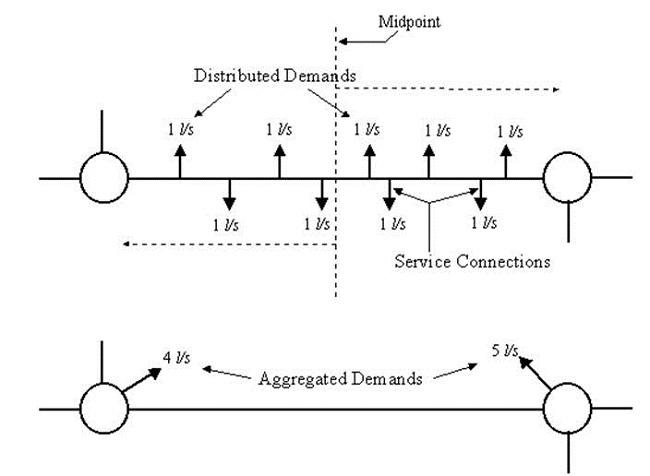
Figure 3 Demand Load Simplification
Most network computer programs today, include both a hydraulic model and a water quality model. The hydraulic computer program solves a set of equations that are used to determine the flows in each of the pipes, the pressures at each of the nodes, and the operational status of various components in the system (e.g. tanks, valves, pumps, etc.). The water quality computer program, uses the results of the hydraulic analysis to solve an additional set of equations that are used to determine the movement and concentration of selected water quality parameters (e.g. chlorine) throughout the system.
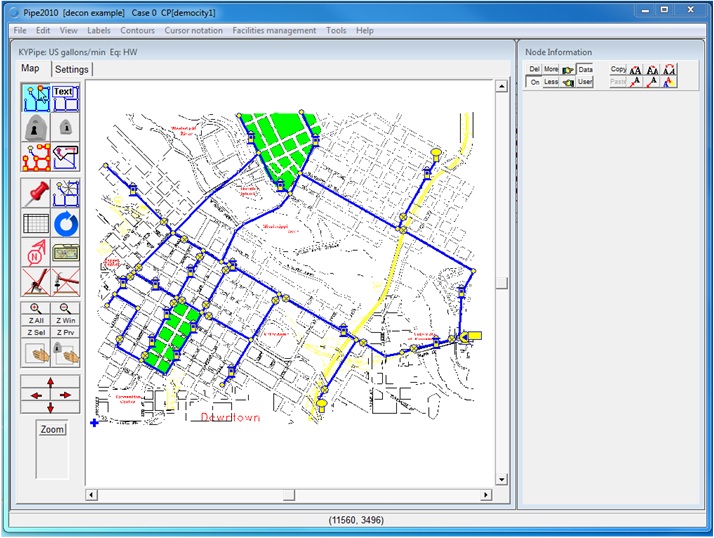
Figure 4 Example of Graphical User Interface (i.e. KYPIPE)
Network Analysis
The application of a network model in the analysis of a water distribution system will normally involve three basic steps: 1) model development, 2) model calibration, and 3) model applications. Each of these steps is discussed in detail in the AWWA Manual M32 (AWWA, 2005). A brief summary of each step is provided below:
Model Development
Developing a network model will normally involve three basic steps: 1) Data gathering 2) Map Development and 3) Computer coding. In developing a network model two different kinds of data must be collected:1) Physical data and 2) Operational data. Physical data include such things as geometric data (i.e. node-pipe linkage), pipe and node data, and initial estimates for pipe roughness and nodal demands. Operational data include such things as the daily pump operating schedule, storage usage, and valve operations. The physical and operational data required for the development of a network model can normally be obtained from maps of the water system, as-built drawings, operational records, and conversations with plant operators and city or utility engineers.
To a certain degree the exact data requirements for a particular computer model will be somewhat dependent upon the options of the program. In general, all programs require a junction label, elevation, and water demand value for each junction node. Similarly, most of program will require a pipe label, beginning and ending junction node labels, pipe length, diameter, and roughness of each pipe. Most programs allow the user to characterize the pipe roughness using either the Hazen-Williams equation or the Darcy-Weisbach equation. Some programs also allow the user to assign a minor loss to each pipe and to characterize various types of control valves (i.e. check valves, pressure regulating valves, pressure sustaining valves, etc.).
Pumps may be simulated using a network model in a variety of ways. For the situation involving a source with a constant head pump, the pump may be simulated as a constant tank. For the situation involving a source with a constant flow pump, the pump maybe simulated be a junction node with negative demand. Variable head pumps can either be simulated using a constant head characterization or by mathematically approximating the pump characteristics curve using some type of curve fit. Most good models have a pump curve fit option as a program feature.
Once the required network data are acquired they are normally recorded on a working map of the system. In order to develop a working map a complete system is first developed. The system map is typically of a scale of 1:1000 and includes street names and topographic contours (Walski 1984). Once the system map is developed a skeletal map may be developed by eliminating pipes of minor influence. Guidelines for skeletonization are provided in the AWWA Manual M32 (1989). In general, small lines which are perpendicular to major trunk lines may be considered for removal. However, all small lines may be necessary if they are near a large supply point (such as a tank) or a large demand center, or if they provide a connection between major mains.
Once a skeletal map has been developed, a working map may be constructed by overlaying the skeletal map with a sheet of tracing paper or mylar and creating the node-pipe linkage required by the computer program. Once this has been done, each junction node and pipe is then numbered and the data associated with each component added to the map. In adding the additional descriptive data to the map it is best to use some type of symbolic index so that numbers associated with different types of data can be so identified.
Model Calibration
Once a network model has been developed, it is imperative that it first be calibrated prior to use. A detailed discussion of model calibration is provided in the AWWA M32 Manual (1989) and by Walski (1984). Model calibration involves the adjustment and/or modification of the mathematical model so that the predicted model results match previously observed conditions. The steps required to properly calibrate a network model are: 1) Develop the network model. 2) Initialize the model parameters, 3) Collect the required calibration data, 4) Perform a micro-level calibration, and if necessary, perform a macro-level calibration.
Once the initial network model has been developed, initial estimates for the pipe roughness and nodal demands should be obtained. Although preliminary estimates of pipe roughness may be obtained from literature values, it is always best to obtain such values directly from field tests of the actual system. Guidelines for such field tests are provided by Walski (1984) and McEnroe et. al.(1989).
The two model parameters that are normally adjusted in a model calibration are the nodal demands and the pipe roughness. In some instances it may be necessary to adjust the model boundary conditions as well (i.e. tank levels, pump heads, PRV settings etc.), however, the values associated with the boundary conditions should normally be determined explicitly from field measurements (such as from recorded charts). The spatial distribution of the nodal demands can be initialized using one of two approaches: a disaggregation approach or an aggregation approach. In the disaggregation approach the total residual demand (i.e. the total demand minus all known major users) is distributed among the junction nodes on the basis of the ratio of the service area of each node to the total service area. In the aggregation approach the residual demand is assigned based on the total number of consumption units associated with each node and the unit demand associated with each consumption unit.
Once initial estimates of the pipe roughness and nodal demands are obtained, a micro-level calibration should be performed. The micro-level calibration involves adjustment of the pipe roughness values and nodal demands until the model accurately predicts flows and pressures in the system for a wide range of operating and loading conditions. In general, two different levels of calibration should be performed: a steady-state calibration followed by a dynamic calibration. In the steady-state calibration the model parameters are adjusted to simultaneously match observed flows and pressures for several different steady-state loading conditions. The observed flows and pressures are normally obtained from fire flow tests. When performing such tests, it is important to make sure that the system is sufficiently stressed to cause a significant drop in pressure; otherwise the fire flow data may be insufficient to allow for proper model calibration (Walski, 1984).
Once the steady state calibration has been performed, a dynamic calibration should follow. The dynamic calibration involves the fine tuning of the model parameters to match observed tank level or flow meter fluctuations over a 24 hour period. Data for this level of calibration can hopefully be obtained from telemetry records. Alternatively the data may have to be collected directly, say, by placing a pressure recorder at the base of a tank.
In general the steady state calibration is more sensitive to adjustments in pipe roughness while the dynamic calibration tends to be more sensitive to the nodal demand. In each case a good calibration model will be one in which the predictive values are within 5-10 percent of the observed values. If the micro-level calibration is unable to produce such results it may be that the model topology or assumed operating conditions are incorrect. In such case it may be necessary to perform a macro-level calibration. That is, it may be necessary to review the underlying assumptions of the original model to determine if any errors are present. An excellent discussion of some of the issues associated with macro-level calibration is provided by Walski (1990).
In recent years several authors have proposed techniques or algorithms for use in calibrating hydraulic network models. These include the use of analytical (Walski 1983) the use of explicit (simulation) algorithms (Ormsbee and Wood 1986) and the use of implicit (optimization) algorithms (Ormsbee 1989 and Lansey and Basnet 1991). Despite the availability of such techniques the trial - and - error method remains the dominant method of use.
Model Calibration Literature
In order for a water distribution model to be truly useful, it needs to accurately reflect real operating conditions. That is, it should accurately reflect current pressures and flows throughout the system, the time it takes to fill or drain a tank and the travel time from one point to another. It should also be able to predict the pressures and status of different components in the system (e.g. tank levels) at some future point in time. In order for a model to be able to do this, it needs to be first calibrated prior to use. Model calibration simply involves the process where the modeler inputs initial estimates for different model parameters such as pipe roughness, nodal demands, pump heads, etc. into the model, executes the model, and then compares the results of the model to actual field observations. If the model results and the field observations do not match, then the modeler will need to go back and adjust the model parameters, rerun the model, and then compare the model results again with the field results. This process may require several iterations until the model is properly calibrated. Several articles which provide specific instructions on how to properly calibrate a hydraulic model are provided below.
-
Ormsbee, L., and Lingireddy, S., (1999) Calibrating Hydraulic Network Models, Journal of the AWWA, 89 (2) pp 42-50. Calibration of Hydraulic Network Models by Lindell and Lingereddy 1997
-
U.S. EPA (2005) Water Distribution System Analysis: Field Studies, Modeling and Management (A Reference Guide for Utilities) EPA/600/R-06/028 Link here.
-
Maslia, M., Sautner, J., (2005) "Use of Continuous Recording Water-Quality Monitoring Equipment for Conducting Water Distribution System Tracer Tests: The Good, the Bad, and the Ugly." Proceedings of the ASCE Water Congress 2005. http://ascelibrary.org/doi/abs/10.1061/40792%28173%2952
-
Walski, Thomas, (1990) "Sherlock Homes meets Hardy Cross", Journal of the AWWA, pp 34-38. http://www.awwa.org/publications/journal-awwa/abstract/articleid/12399.aspx
-
Grayman, W., Morris, M., and Sautner, J., (2006) Calibrating Distribution System Models with Fire-Flow Tests, Opflow, April, pp. 10-12. http://www.awwa.org/publications/opflow/abstract/articleid/18136.aspx
Laboratory Model Calibration Case Study
Use of computer models (both hydraulic and water quality) to aid in the operations of water distribution systems in a real-time environment requires that the models represent the actual system as accurately as possible. In the past, such models have frequently incorporated basic physical assumptions and/or approximations, that while adequate for most static applications (e.g. network design, etc.), may introduce levels of errors that could prove to be significant when applied in support of real time operations and in particular in support of contamination detection. As an example Wood et al., (1993, 1994) have shown that the use of a constant minor loss coefficient for pipe junctions and fittings may introduce a significant error in network modeling results, especially in the case of large diameter pipes with short lengths. The impact of such errors on water quality predictions is largely unknown. As part of their research, Wood et al. (1993) developed flow dependent loss relationships for several different standard fitting configurations that could be incorporated into most standard hydraulic software.
In addition to explicit hydraulic considerations, several researchers (Lee and Buchberger, 2001; Tzatchkov et al., 2002; and Lee, 2004) have shown that dispersion can have a significant effect on concentration profiles, especially in the case of intermittent laminar flow. Further, Buchberger et al., (2003) have shown that the aggregation and concentration of distributed system demands at junction nodes can also impact water quality predictions. Finally, Van Bloemen Waanders et al. (2005) have shown that the normal assumption of complete mixing at junction nodes, such as made in EPANET, is not totally accurate, especially at four pipe intersections. In order to evaluate the impacts of each of the such assumptions on the ability of hydraulic (and by dependence water quality) models to accurate forecast future state conditions, a laboratory scale model of a water distribution network was constructed and its performance compared to that of hydraulic and water quality computer models.
The laboratory model for use in this study was based on an actual water distribution system in Kentucky. Following the identification of the utility, a site visit was conducted and relevant system data collected, including data associated with the hydraulic model for the system, as well as operational field data for use in developing and calibrating a water quality model for the system. Using the collected data, a scale representation of the system was constructed in the hydraulics laboratory of the University of Kentucky, such that both network hydraulics and fate and transport processes are represented as accurately as possible. The developed model was instrumented with basic flow and pressure sensors as well as the capability to evaluate surrogate water quality parameters (e.g. food grade calcium chloride). The model was also be instrumented with inline valves for use in adjusting the relative head-loss associated with each pipe segment.
Once constructed, hydraulic and water quality models of the system were developed and calibrated using data collected from the physical laboratory model using standard EPA protocols (2005) as modified for laboratory applications. Once calibrated, the computer models were used to forecast future hydraulic and water quality conditions based on the known boundary conditions of the physical model. The observations from the physical model were compared with the predictions of the computer models in order to assess the reliability of the computer models to accurately predict the observed conditions. The sensitivity of the measured water quality parameters to system hydraulics were determined by varying the boundary and loading conditions of the physical model and then determining the impacts on the water quality results. Once determined, the ability of the computer models to replicate these results was evaluated.
Following these analyses, an attempt will be made to calibrate the laboratory model to the actual utility water distribution network by adjusting the pipe roughness and system demands (of the laboratory physical model) using inline roughness values and demand outlet values respectively. A dimensional analysis of the critical network parameters will be performed in order to provide guidance with regard to scaling factors for application to the laboratory model. If successful, the ability of the computer models to replicate the hydraulic and water quality performance of the calibrated laboratory model will then be explored. Once again, it is anticipated that these analyses may yield useful insights on the relative impact of flow dynamics on water quality and the ability of computer models to accurately predict such impacts.
A copy of the final report which documents the construction and application of the model is provided through the links below:
Actual System Calibration Case Studies
As part of the research project, hydraulic simulation models were developed for a small and moderately sized water utilities in Kentucky. A water quality model was also developed for the moderately sized utility. Both of the hydraulic models were calibrated prior to use. The water quality model was also calibrated. In addition, a large water utility was also calibrated as part of the real-time model study of the project. Reports on each of these calibration studies can be obtained from the links below:
In addition to these studies, the CDC recently completed a water quality study of the Camp Lejeune Marine Base. A copy of this report can be obtained from the link below:
Model Application
Once a computer model of the water distribution system has been created and calibrated, the operator has an extremely powerful tool at his or her disposal. The operator can use the model to assess the performance of the existing system and/or identify and locate system inadequacies. If system inadequacies are identified the model can then be used to evaluate the impact of any proposed design improvements.
Most available computer network models may be applied in either a steady state or an extended period simulation. In most models the extended period simulation is automatically performed by linking or integrating a series of discrete steady state analyses. Steady state simulations provide a snapshot analysis for determining pressures and flows for specified demands, tank levels, and pump operations. Extended period simulations allow for an evaluation of the performance of the system over time. Such an analysis may be important in evaluating performance of tanks in the system in response to extended fire demands, specific pump operating policies, or a basic 24 hours diurnal demand pattern.
Examples of Model Applications
Water distribution computer models can be used in support of a wide range of applications. These include;
Planning
-
Capital improvement planning
-
Conservation impact studies
-
Water main rehabilitation evaluation
-
Siting of future storage tanks
Engineering Design
- Fire flow studies
- Valve sizing
- Reservoir sizing
- Pump station sizing
- Pipe sizing
- Calculation of pressures and flows at particular locations
- Pressure zone boundary identification
System Operations
- Personnel training
- Troubleshooting
- Water loss calculations
- Emergency operation scenarios
- Source management
- Main flushing
- Energy cost management
Water Quality Improvement
- Constituent tracking
- Water source/age tracking
- Chlorine levels
- Water quality monitoring location
Real Time Operations
- Scenario forecasting
- Optimal pump scheduling
- Event detection
Model Selection
Computer models for water distribution analysis have been available since the late sixties (Ormsbee, 2006). Over the last fifteen years, such models have been augmented with very sophisticated pre and post processing software including GIS interfaces and customized graphical user interfaces (GUIs). When selecting a potential computer program the buyer should consider several things. Among the more important issues are: 1) ease of data input, 2) geometric data requirements, 3) program options, 4) numerical stability and reliability, 5) graphical interface capabilities, 6) program history, 7) cost, and 8) user support. Two of the more widely used computer programs, and in particular for small to medium sized utilities are EPANET and KYPIPE.
EPANET
EPANET was developed by researchers at the EPA Risk Management Laboratory in Cincinnati primarily as a water quality model. While EPANET has emerged as the model of choice for academicians, primarily due to its open source architecture, its application to actual water utility systems has been somewhat limited. This is due to several factors, including the lack of any formal support structure or training programs. Secondly, EPA does not have a formal program to provide continual upgrades to its user interface, which hinders its sustained use in the water utility arena. Free copies of EPANET may be downloaded off the internet at the EPANET website:
KYPIPE
KYPIPE was originally developed at the University of Kentucky in the early seventies, making it the oldest hydraulic software that is still commercially available. Technical support for the software is provided free, making it especially attractive software for small utilities. Free demo versions of the program are available at the KYPIPE website. For larger applications, the cost of the software is related to the size of the system. The KPIPE website is:
References
AWWA (American Water Works Association). (1989). “AWWA Manual M32-Distribution Network Analysis for Water Utilities.” 1st Ed. Denver, CO: AWWA.
AWWA (American Water Works Association). 2005. “AWWA Manual M32-Computer Modeling of Water Distribution Systems.” 2nd Ed. Denver, CO: AWWA.
Buchberger, S.G., J.T. Carter, Y. H. Lee, and T. G. Schade. (2003). “Random Demands, Travel times, and Water Quality in Deadends.” AWWA Research Foundation. Denver, CO.
Lansey, K., and Basnet, C. (1991). "Parameter Estimation for Water Distribution Networks." ASCE Journal of Water Resources Planning and Management, 117(1), 126-145.
Lee, Y. (2004). “Mass Dispersion in Intermittent Laminar Flow.” Ph.D. Dissertation in Civil and Environmental Engineering, University of Cincinnati, Cincinnati, OH.
Lee, Y. and S. G. Buchberger. (2001). “Estimation of dispersion in unsteady random flow conditions in dead-end pipes of water distribution systems.”Proceedings, ASCE-EWRI World Water & Environmental Resources Congress, Orlando, FL.
McEnroe, B., D. Chase, and W.Sharp. (1989). “Field Testing Water Mains to Determine Carrying Capacity.” Technical Paper EL-89, Environmental Laboratory of the Army Corps of Engineers Waterways Experiment Station, Vicksburg, MS.
Ormsbee, L.E. and Wood, D.J. (1986). "Explicit Pipe Network Calibration." ASCE Journal of Water Resources Planning and Management, 112(2), 166-182.
Ormsbee, L.E. (1989). "Implicit Pipe Network Calibration." ASCE Journal of Water Resources Planning and Management, 115(2), 243-257.
Ormsbee, L. (2006). “The History of Water Distribution Modeling.” Proceedings of the ASCE Water Distribution Specialty Conference, Cincinnati, OH.
Tzatchkov, V. G., A.A. Aldama, and F.I. Arreguin. (2002). “Advection-dispersion Reaction Modeling in Water Distribution Networks.” Journal Water Resources Planning & Management, 128(5): 334-342.
US EPA. (2005). “Water Distribution System Analysis: Field Studies, Modeling and Management - A Reference Guide for Utilities.” EPA/600/R-06/028, Cincinnati, OH.
Van Bloemen Waanders, B., B. G. Hammond, J. Shadid, S. Collis, and R. Murray. ( 2005). “A Comparison of Navier-Stokes and Network Models to Predict Chemical Transport in Municipal Water Distribution Systems.” Proceedings , ASCE - EWRI World Water and Environmental Resources Congress, Anchorage, AK.
Walski, T.M. (1990). “Sherlock Holmes Meets Hardy Cross, or Model Calibration in Austin, Texas.” Journal American Water Works Association, 82(3): 34-38.
Walski, T.M. (1984). “Analysis of Water Distribution Systems.” Van Nostrand Reinhold Co., New York, NY, USA.
Walski, T.M. (1983). “Technique for calibrating network models.” Journal of Water Resources Planning and Management, 109(4): 360-372.
Wood, Don J., L. Srinivasa Reddy, and J. E. Funk. (1983). "Modeling pipe networks dominated by junctions." Journal of Hydraulic Engineering, 119(8): 949-958.
Wood, D. J., L. S. Reddy, and J. E. Funk. (1994). "Incorporating flow dependent loss coefficients into pipe network models." Integrated computer applications in water supply (vol. 1). John Wiley & Sons, Inc..